Best Non GamStop Casinos for UK Players in 2025
🖊️ Written by Mario Nawalif
Gambling Expert with 25 Years of Real-World Experience
If you’re looking for trusted non GamStop casinos that combine quality, flexibility, and security, you’ve just found the right destination. Whether your goal is to bypass the restrictions of GamStop or simply enjoy a broader range of gaming options, our in-depth coverage connects UK players with the top-rated online casinos not on GamStop—all handpicked by experts with years of experience in the iGaming space.
In a market flooded with offshore platforms making bold promises, it’s easy to feel lost. That’s where we come in. Our team carefully vets each non GamStop casino site, evaluating key criteria such as licensing credibility (like Curaçao or Kahnawake), payout reliability, data protection, game fairness, and payment versatility—including crypto, e-wallets, and more.
We don’t just list casinos—we break them down, test them rigorously, and spotlight the ones that genuinely deliver a safe, fast, and enjoyable experience. Whether you’re a seasoned player or exploring your options outside the UKGC system for the first time, our mission is simple: to help you gamble smarter, not harder.
- Best Non GamStop Casinos for UK Players in 2025
- Best rankings of Non Gamstop Casinos
- How We Choose the Best Casinos Not on GamStop: Our Trusted Review Process
- You’re In! Step-by-Step Guide to Getting Started at a Non GamStop Casino
- Pros & Cons of Playing at Casinos Not on GamStop
- How to Fund Your Gameplay: Payment Options at Non GamStop Casinos
- Game Selection at Non GamStop Casinos: What to Expect from Top Platforms
- Top Casino Bonuses You’ll Find at Non GamStop Sites
- First-Time Deposit Offers: Kickstart Your Gaming With a Bang
- No Deposit Rewards: Try Before You Commit
- Free Spins Promotions: More Spins, More Wins
- Crypto Bonuses: Bigger Perks for Digital Currency Players
- Cashback Deals: Win Back a Portion of Your Losses
- Reload Bonuses: Extra Value for Returning Players
- VIP Clubs & Loyalty Programs: Elite Perks for Dedicated Players
- Unlock More Value with Non GamStop Casino Bonuses
- Final Thoughts: The Advantages of Choosing Non GamStop Casinos
- Frequently Asked Questions
Best rankings of Non Gamstop Casinos
Our expert team of iGaming professionals rigorously tests and reviews each non GamStop casino before it earns a spot on our list. We assess everything—from game variety and user experience to payout speed and customer support. Only the most reputable and secure platforms make the cut.
Ready to explore the best non GamStop casinos that deliver real value and endless entertainment? Let’s dive in and find your perfect place to play.
🥇 Magic Red Casino (Non Gamstop Version)
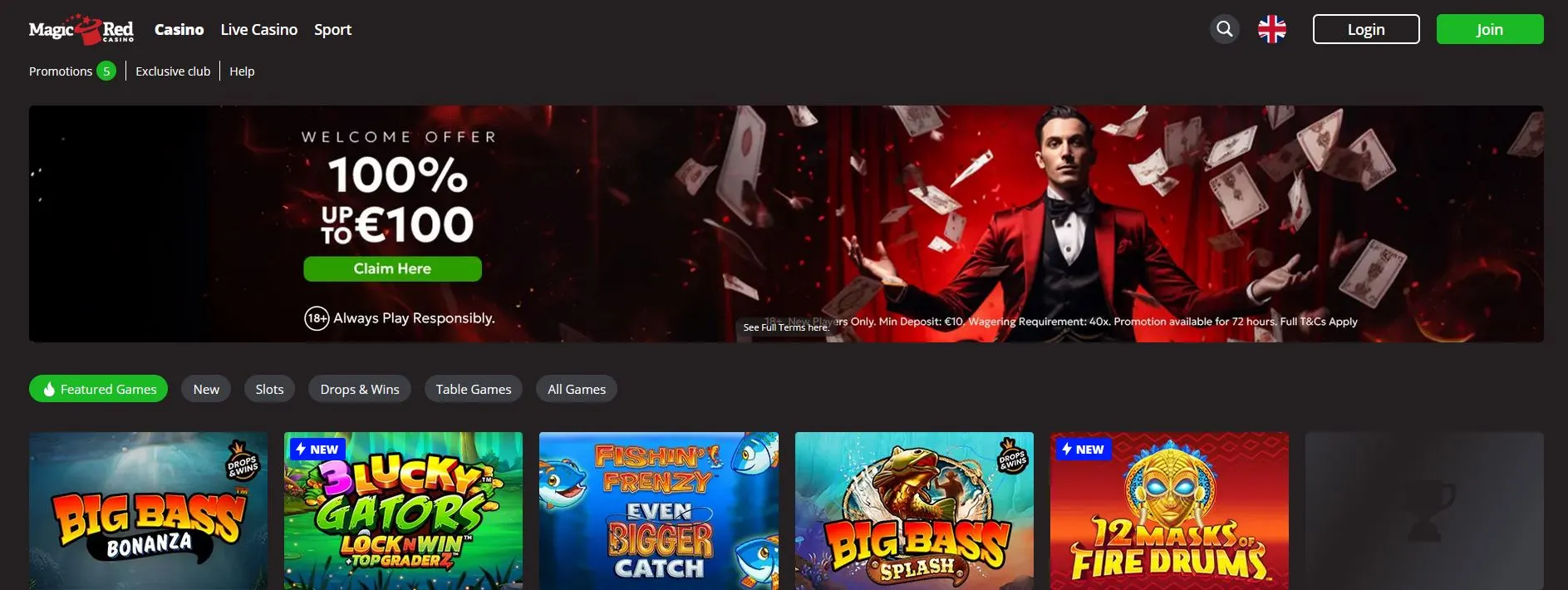
I’ve spent over 25 years in the gambling world, and let me tell you—Magic Red Casino has always been a name you can rely on. But their non GamStop version? That’s something else entirely. Think of it as a VIP shortcut to the same premium experience—minus the red tape that comes with UKGC restrictions.
I tested the offshore Magic Red Casino firsthand, and the process was refreshingly smooth. No ID uploads. No drawn-out verifications. Just a clean, one-click sign-up and I was in. I grabbed their 250% welcome bonus (which actually delivered real value) and jumped into the action. The games lineup is solid—NetEnt, Microgaming, Play’n GO—all the industry heavyweights. And performance-wise? Flawless. No lag, no freezes, even when switching between live tables and classic slots.
Their sportsbook is another standout—football, horse racing, basketball, the works. What really sets it apart? No stake limits and no surveillance-style restrictions. You bet how you want, when you want. When I was ready to cash out, I used Skrill, and the funds landed in my account within hours. No delays. No nonsense.
In short, this is the Magic Red Casino you remember—just freer, faster, and far more flexible. If you’re after a reliable non GamStop casino with big bonuses, top-tier games, and hassle-free withdrawals, this one’s a no-brainer.
✅ Pros of Magic Red Casino:
- Big-name reputation with offshore flexibility
- 250% welcome bonus with real payout potential
- No KYC or ID checks required to play or withdraw
- Optimized for both mobile and desktop gaming
❌ Cons of Magic Red Casino:
- Not accessible via the UK homepage—requires offshore link
- UK debit cards not accepted directly (use eWallet or crypto)
💳 Payment Methods: Skrill, Neteller, bank transfer, Bitcoin, Ethereum, Tether
🥈 Bet365 Casino (International Non Gamstop Exchange)
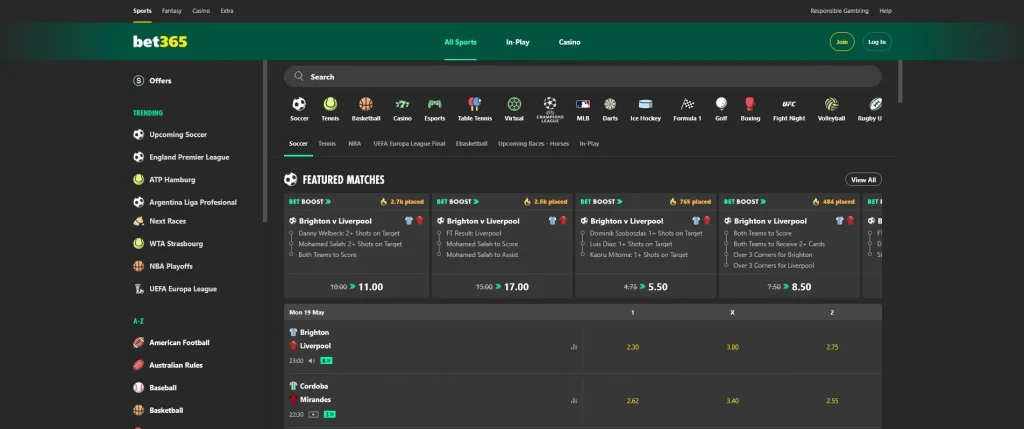
I’ve been part of the gambling industry for 25 years, and few brands carry the same legacy as Bet365. Known for its unmatched sportsbook and vast gaming catalogue, Bet365 remains one of the most respected names in online betting. But here’s the reality check: because it’s fully licensed by the UK Gambling Commission, Bet365 is part of the GamStop self-exclusion program—which means there’s no official non GamStop version of the site.
That said, if you’re not registered with GamStop or you’re simply looking for a highly reliable, regulation-compliant platform, Bet365 still delivers one of the best betting experiences in the UK.
During my latest test run, everything from sign-up to gameplay was seamless. The casino section features titles from major providers like NetEnt, Playtech, and Pragmatic Play, while the sportsbook is every punter’s dream—covering everything from Premier League football to Formula 1, darts, tennis, and global events.
One highlight that stood out was their “10 Days of Spins” offer—up to 200 free spins with no wagering requirements. That’s right: what you win is yours, no strings attached. It’s a rare perk in an industry full of complicated rollover terms.
When it comes to payments, Bet365 supports Skrill, Neteller, PayPal, and traditional bank methods. Withdrawals—especially via e-wallets—are typically processed within hours, making it one of the more efficient platforms for cashing out.
✅ Pros of Bet365 Casino:
- Established reputation with a wide range of offerings
- “10 Days of Spins” welcome offer with no wagering requirements
- Efficient payment methods, including e-wallets and bank transfers
- Optimized for both mobile and desktop gamingCasino.org+4Casino.org+4Dimers+4
❌ Cons of Bet365 Casino:
- Operates under UKGC regulations, meaning it’s part of the GamStop program
- Strict KYC procedures required for account verification
💳 Payment Methods: Skrill, Neteller, bank transfer, debit/credit cards
For players seeking platforms outside the GamStop scheme, it’s advisable to explore other licensed offshore casinos that cater to such preferences.
🥉 Betmorph Casino (Non Gamstop Casino Extension)
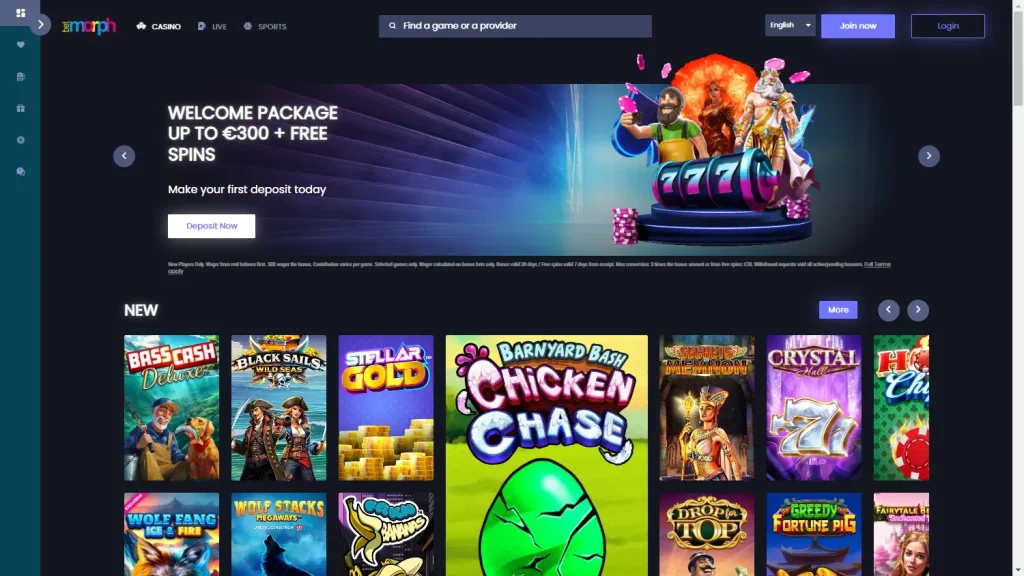
Betmorph might not have the household name of giants like PaddyPower or Betfair, but don’t let that fool you—this non GamStop casino is one of the most player-focused platforms I’ve come across in the past year.
I first discovered Betmorph while searching for a no-verification crypto casino that actually pays out fast—and I wasn’t disappointed. The registration took seconds. No ID upload. No drawn-out checks. Just a clean, frictionless sign-up. I deposited via Litecoin, though they accept a wide range of options including Bitcoin, Ethereum, and eWallets, and snagged a generous 300% welcome bonus—with no hidden terms.
The user experience is tight. Fast load times, an intuitive layout, and a cashier that actually works without making you jump through hoops. But what really sets Betmorph apart is its game selection. Expect a mix of Booongo, Spinomenal, and Betsoft—providers you rarely see on UKGC-regulated platforms. It’s a fresh, international lineup that offers something genuinely different.
Over the course of a week, I played everything from blackjack to niche slot titles, and every one of my five withdrawals landed in under 12 hours—no bonus traps, no sudden KYC requests, just smooth, crypto-friendly payouts.
✅ Pros of Betmorph Casino:
- Massive 300% welcome bonus with fair terms
- No ID or document uploads ever
- Supports a wide variety of crypto coins
- Withdrawal speed is consistent and fast
❌ Cons Betmorph Casino:
- Smaller brand, less reputation history
- Doesn’t offer a sportsbook (casino only)
💳 Payment Methods: Bitcoin, Ethereum, Litecoin, Tether, Jeton, MuchBetter, AstroPay
🔗 [Read full review]
🏅 Betfred Casino (Non GamStop Site)

Betfred’s offshore casino hit me right in the nostalgia. I remember the buzz of walking into their high street shops for a cheeky bet—and this version? It’s got that same old-school edge, only without the UKGC handcuffs.
Signing up was effortless: no GamStop barriers, no document uploads—just a quick email and password, and I was in. I deposited using AstroPay (though they also support Jeton, crypto, and eWallets), and the funds landed instantly. But what really stood out? The freedom. No stake limits. No pop-ups pushing “safer gambling tools.” Just uninterrupted gameplay, the way it used to be.
Their 150% welcome bonus even threw in a £10 free bet, which I casually dropped on a football double—landed perfectly. But this isn’t just about sports. The casino side is stacked too: slots, bingo, live dealers, and yes, even their bingo rooms still have that Betfred energy. I cashed out £200 via Jeton, and it hit my account in under 24 hours. No chasing. No random checks. Just straight-up efficiency.
If you’ve been craving that classic Betfred experience without UK restrictions, this offshore version delivers. It’s fast, familiar, and refreshingly free of the red tape. Whether you’re after sports, slots, or bingo, Betfred Non GamStop Casino blends nostalgia with modern convenience—and it does it brilliantly.
✅ Pros of Betfred:
- Classic Betfred brand with modern freedom
- Sports, bingo, live casino, all under one roof
- Accepts UK-friendly payment methods
- Low deposit minimums
❌ Cons of Betfred:
- Smaller bonus compared to competitors
- No PayPal support yet
- Delays on Withdrawals
💳 Payment Methods: AstroPay, Jeton, Bitcoin, Litecoin, Skrill, Neteller
How We Choose the Best Casinos Not on GamStop: Our Trusted Review Process
Exploring the world of casinos not on GamStop can feel like navigating uncharted waters. With so many offshore platforms promising the best experience, it’s easy to get overwhelmed—or worse, fall into the trap of unreliable operators. That’s why we’ve developed a clear, expert-driven review process to identify and recommend only the most reputable, high-performing non GamStop casinos.
Our mission is simple: to help players find safe, fair, and rewarding alternatives to UKGC-licensed sites, without sacrificing security or entertainment. Here’s what sets the best non GamStop casinos apart.
True Gaming Freedom, No GamStop Restrictions
One of the key advantages of playing at casinos not registered with GamStop is the ability to bypass the UK’s self-exclusion system. These platforms give players complete access to games, bonuses, and betting features, without being locked into GamStop’s limitations. Whether you’re chasing higher limits or seeking more personal control over your play, these sites offer unmatched freedom—and that’s a core part of our review criteria.
A World-Class Game Library
Game variety matters. The best non GamStop casinos host an impressive selection of slots, table games, and live dealer content from top-tier providers like Playtech, Betsoft, and Microgaming. From immersive video slots to poker rooms and roulette tables, we look for casinos that cater to all player types, with consistently high-quality performance and fair RNG outcomes.
Mobile-Ready for Seamless Play Anywhere
A top casino in 2025 needs to perform just as well on mobile as it does on desktop. Our recommended sites are fully mobile-optimized, ensuring fast load times, smooth navigation, and full access to the game library—whether you’re on iOS, Android, or a tablet. No apps required, no compromises.
Big Bonuses and VIP Treatment
Generous promotions are another major selling point for non GamStop casino sites. We favour platforms that offer more than just a flashy welcome bonus. Ongoing deals like free spins, cashback offers, reloads, and VIP perks are all indicators of a casino that values player loyalty. We also check for fair terms—no outrageous wagering requirements or fine print traps.
Proper Licensing and Player Safety
Just because a casino isn’t on GamStop doesn’t mean it should be risky. We only recommend platforms licensed by reputable offshore authorities such as Curaçao eGaming or Anjouan. These sites employ SSL encryption, protect user data, and undergo independent audits to ensure transparency and fairness. Security is non-negotiable in our review process.
Why It Matters
By focusing on these essential factors—freedom, game quality, mobile performance, bonus value, and licensing—we help players cut through the noise and find the most reliable non GamStop casinos available today. Whether you’re returning to gambling after a GamStop self-exclusion or simply seeking greater flexibility, our expert guides and hands-on reviews offer a safe and informed path forward.
You’re In! Step-by-Step Guide to Getting Started at a Non GamStop Casino
Welcome aboard—you’ve just signed up with one of the top non GamStop casinos, and you’re now just minutes away from playing your favorite games without restrictions. Whether you’re a seasoned bettor or trying out offshore casinos for the first time, this guide will help you get started smoothly and confidently.
Step 1: Register Your Account
Start by creating your player profile. Head to the casino homepage and click “Join Now” or “Register”. The signup process is quick and simple—usually just the following:
- Full name (must match your payment details)
- Email address (used for verification and bonus updates)
- Date of birth (to confirm you’re 18+)
- Username & password (keep them secure)
Some casinos will email you a confirmation link—click it to activate your account and unlock full access.
Step 2: Make Your First Deposit
With your account ready, it’s time to add funds. Non GamStop casinos support a variety of flexible payment methods, including:
- Credit/Debit Cards – Visa, Mastercard, and others
- E-wallets – Skrill, Neteller, ecoPayz for fast, secure deposits
- Cryptocurrencies – Bitcoin, Ethereum, Litecoin for privacy and speed
- Prepaid Cards – Neosurf, PaySafeCard for extra spending control
Enter your desired amount, confirm the payment, and your balance will update instantly.
Step 3: Claim Your Welcome Bonus
Most casinos not on GamStop offer generous welcome packages to get you started. Common promos include:
- Deposit match bonuses (e.g., 200% or 300% match)
- Free spins on popular slots
- Cashback deals on losses
Visit the Promotions section, follow any opt-in steps, and check bonus terms—especially wagering requirements and validity.
Step 4: Choose Your Game and Start Playing
Now for the fun part. Non GamStop casinos host a huge selection of real-money games:
- Slots – Jackpot titles, Megaways, and high-RTP favorites
- Table Games – Blackjack, roulette, baccarat, and more
- Live Casino – Play with real dealers via HD streams
- Sports Betting – Place bets on football, tennis, boxing, and global markets
Explore the full lobby to find the games that match your mood and strategy.
Step 5: Play Responsibly
Freedom comes with responsibility. Non GamStop casinos don’t enforce UKGC tools, so it’s up to you to manage your gameplay wisely:
- Set personal limits for deposits, losses, and time
- Stick to your budget—don’t gamble more than you can afford
- Take regular breaks to stay focused
- Use built-in tools if available (self-exclusion, deposit caps, etc.)
Smart play leads to more enjoyment and longer-lasting wins.
Final Word: Enjoy the Ride
Now that you’re fully set up, you’re ready to experience the best that non GamStop casinos have to offer—bigger bonuses, more freedom, faster payments, and a world-class gaming experience. Play smart, stay safe, and have fun.
Pros & Cons of Playing at Casinos Not on GamStop
Non GamStop casinos are increasingly popular with UK players looking for more control, larger bonuses, and fewer restrictions. These offshore platforms offer a flexible, fast-paced alternative to UKGC-licensed sites. But with that freedom comes a few trade-offs. Below, we break down the key advantages and disadvantages to help you decide if non GamStop casinos are right for you.
✅ What Makes Non GamStop Casinos a Popular Choice
Total Gaming Freedom with No Limits
Unlike UK-licensed casinos, non GamStop sites don’t impose deposit caps, wagering limits, or mandatory timeouts. This freedom appeals especially to high-stakes players or anyone frustrated by over-regulation. Whether you’re spinning slots or betting big at the tables, you’re in full control of your experience.
Fast Registration with No KYC Hassle
Signing up is quick and painless. Most platforms don’t require ID verification upfront, which means no document uploads or waiting around. All you need is a valid email and password—letting you jump into the action instantly while keeping your privacy intact.
Bigger Bonuses with Fewer Strings
Offshore casinos can offer much larger promotions because they aren’t bound by UKGC advertising rules. You’ll often find:
- 200%+ welcome bonuses
- Cashback on losses
- Free spins with no wagering requirements
That means more playtime, more rewards, and far fewer hoops to jump through.
Flexible Payment Options, Including Crypto
Payment variety is a major plus. Non GamStop casinos typically accept:
- Visa, Mastercard, Maestro
- E-wallets like Skrill, Neteller, ecoPayz
- Cryptocurrencies such as Bitcoin, Ethereum, Litecoin
- Prepaid vouchers and even bank transfers
Credit cards are often accepted too—something UKGC sites now prohibit.
Massive Game Libraries from Top Global Providers
These casinos partner with international software developers, offering a broader range of games than most UK operators:
- Slots: Megaways, jackpots, and high-RTP hits
- Table Games: Blackjack, baccarat, roulette, poker
- Live Dealers: Real casino action via HD streams
- Sports Betting: Many sites include full sportsbooks and even esports markets
If variety matters to you, non GamStop casinos typically go above and beyond.
⚠️ Things to Consider: The Drawbacks of Non GamStop Casinos
No UKGC Protection
Non GamStop casinos are not licensed by the UK Gambling Commission, which means you won’t have access to UK-specific protections like the GamStop scheme, ADR (alternative dispute resolution), or the UK ombudsman. If something goes wrong, resolution options may be limited.
Risk of Irresponsible Gambling
The lack of deposit limits, timeouts, and self-exclusion features can be dangerous for players prone to problem gambling. These platforms place the responsibility entirely on the player—so it’s crucial to set your own limits and play with discipline.
Licensing Quality Varies
While some non GamStop casinos are licensed by reputable bodies like Curaçao eGaming or Anjouan, others operate with less oversight. Always research the license and operator before depositing funds.
Fewer Responsible Gambling Tools
These casinos generally don’t offer the same support features found on UK sites—such as gambling history logs, self-assessment tools, or access to services like GAMSTOP, GamCare, or BeGambleAware.
Final Verdict
Non GamStop casinos offer a high-reward, high-freedom gaming environment ideal for players who value control, fast sign-ups, and big bonuses. But they also come with more personal responsibility. As long as you play smart and stick with well-reviewed, licensed operators, these platforms can offer a unique and exciting alternative to traditional UK casinos.
Things to Keep in Mind Before You Play
No Built-In Self-Exclusion Programs
One of the biggest risks of non GamStop casinos is the lack of enforced responsible gambling measures. These sites aren’t part of the UK’s national self-exclusion scheme, so if you’re struggling with gambling control, the freedom can be dangerous. There are no automatic timeouts or deposit caps—you’ll need to self-regulate your play.
Limited Responsible Gaming Tools
While some non GamStop platforms offer voluntary limits, most lack the full suite of tools you’d find on UKGC sites:
🚨 No mandatory deposit limits
⏳ Few session reminders
🚫 No official self-exclusion options
This puts the responsibility squarely on the player. If you value built-in safety nets, these casinos might not be the right fit.
Offshore Licenses with Varying Oversight
Non GamStop casinos are usually licensed in jurisdictions like:
🛡️ Curacao eGaming
🏝️ Anjouan Gaming Authority
🌎 Other lesser-known international bodies
While many of these sites are legitimate, offshore regulation tends to be more relaxed. This can lead to:
Slower payouts
Fewer dispute resolution options
❌ Varying fairness standards
That’s why it’s essential to choose well-reviewed, reputable casinos with a strong track record for transparency and player support.
Potential Issues with UK-Based Banking
Even though non GamStop casinos support a wide variety of payments, UK banks may block transactions to offshore operators. You might also face:
📉 Longer withdrawal times
🚫 Limited access to UK-friendly e-wallets
🔁 Delays in receiving winnings from some sites
To avoid hiccups, it’s a good idea to check the casino’s banking page and see which methods are available for UK players.
Final Verdict: Know the Trade-Offs, Play with Confidence
Non GamStop casinos offer unbeatable freedom, juicy bonuses, and a massive range of games—but that freedom comes with responsibility. If you’re comfortable managing your own limits and choosing trusted offshore operators, these platforms can deliver an exhilarating and rewarding gaming experience. Just do your research, set boundaries, and play smart!
How to Fund Your Gameplay: Payment Options at Non GamStop Casinos
When choosing a non GamStop casino, one of the most important aspects to consider is how you’ll deposit and withdraw your money. The right payment method not only ensures faster transactions and enhanced security but also plays a big role in your overall gaming experience. Unlike UKGC-licensed platforms, non GamStop casinos often support a wider variety of payment methods, giving you more flexibility and freedom to play your way.
Popular Banking Methods You Can Use at Non GamStop Casinos
Since non GamStop casinos serve players from all over the world, they offer a diverse range of banking solutions to suit different preferences and needs. From traditional cards to cutting-edge cryptocurrencies, here’s what you can expect:
Credit & Debit Cards
Visa, MasterCard, and American Express are still some of the most widely used payment options. They’re reliable, easy to use, and allow for instant deposits. However, some UK-based banks may block withdrawals back to cards, so it’s wise to have an alternative cash-out method ready.
E-Wallets
Digital wallets like Skrill and Neteller are popular for their speed and enhanced privacy. They let you move money quickly without sharing your banking details with the casino. While PayPal is rarely supported on non GamStop sites, Skrill and Neteller are widely accepted and typically involve minimal fees.
Cryptocurrencies
Want complete privacy and lightning-fast transactions? Bitcoin, Ethereum, Litecoin, and Tether are becoming the go-to options for many players. These blockchain-based payments offer anonymity, low transaction costs, and instant processing. Some casinos even offer crypto-exclusive bonuses, making this option even more appealing.
Prepaid Cards & Vouchers
Services like PaySafeCard and Neosurf let you fund your account without sharing any personal or financial information. These are perfect for players who value anonymity, though keep in mind they typically don’t support withdrawals—you’ll need a backup method to cash out your winnings.
Mobile Payment Apps
Options like Apple Pay and Google Pay offer secure, one-touch deposits straight from your phone. These mobile-first solutions are quick, safe, and use features like biometric authentication to protect your transactions.
Bank Transfers & Wire Payments
Prefer traditional banking? SEPA transfers, SWIFT payments, and other direct bank options are also available. They’re great for high-stakes players looking to move larger amounts of money. Just note that processing times can be longer, especially for withdrawals.
Payment Methods That May Be Limited or Unavailable
Even though non GamStop casinos offer impressive flexibility, there are still a few payment methods that are less commonly supported:
UK Bank Transfers – Some British banks block payments to offshore casinos, making direct transfers unreliable.
PayPal – Due to strict regulations, PayPal is rarely available on non GamStop gambling sites.
Certain Credit Card Transactions – Some financial institutions automatically block gambling-related charges depending on your location and card provider.
Choosing the Right Payment Method: What to Look For
Before you fund your account, take a moment to evaluate the best option based on your preferences and priorities. Here are a few things to consider:
Speed – For the fastest deposits and withdrawals, go with cryptos or e-wallets.
Privacy – If anonymity is important, prepaid cards and crypto are your best bets.
Fees – Some methods (like credit cards or wire transfers) may include higher fees. E-wallets and crypto usually offer lower-cost alternatives.
Withdrawal Limits – Check the casino’s policies—some payment methods have stricter daily or weekly limits, which may impact frequent players or high rollers.
Review Payment Options Before You Play
Non GamStop casinos shine when it comes to banking flexibility, offering everything from cryptocurrencies to mobile wallets. But no matter which site you choose, it’s crucial to check the deposit and withdrawal terms before registering. This helps you avoid unexpected fees, delays, or restrictions—so you can focus on what really matters: enjoying your gameplay with peace of mind.
Game Selection at Non GamStop Casinos: What to Expect from Top Platforms
One of the biggest draws of non GamStop casinos is the diverse and feature-rich game libraries they offer. With thousands of titles spanning various genres, these casinos cater to players of all experience levels and preferences. Powered by both well-established and up-and-coming software providers, non GamStop sites deliver a premium gaming experience with high-quality visuals, smooth gameplay, and fair mechanics. Whether you’re spinning reels, testing your skills at the tables, or joining live dealer sessions, there’s no shortage of entertainment.
Slot Machines: The Heartbeat of Non GamStop Platforms
Slot games are a cornerstone of every non GamStop casino, and the variety available is staggering. From high-octane Megaways titles to relaxing classic fruit machines, there’s something for everyone.
- Feature-Rich Gameplay – Expect advanced slot mechanics like cascading reels, expanding wilds, bonus buy-ins, and interactive mini-games.
- Massive Jackpots – Progressive jackpot slots such as Mega Moolah, Divine Fortune, and Age of the Gods regularly offer life-changing wins.
These slot titles often include high volatility options that appeal to risk-takers, as well as low-stakes games perfect for casual players looking for entertainment without pressure.
Table Games: A Classic Casino Experience with a Modern Twist
For players who appreciate strategic gameplay, table games at non GamStop casinos offer countless variations of the classics. These digital versions replicate the thrill of land-based casinos while adding modern enhancements.
- Blackjack – Play single-deck, multi-hand, or themed versions like Lightning Blackjack with side bets and fast-paced rounds.
- Roulette – Choose from European, French, and American formats or explore game-changing options like Quantum Roulette with boosted payouts.
- Poker & Baccarat – From Texas Hold’em and Caribbean Stud to Speed Baccarat, these games combine chance and strategy for engaging play.
Top-tier developers such as Playtech, NetEnt, and Play’n GO ensure smooth graphics, realistic animations, and fair RNG outcomes.
Live Dealer Games: Real-Time Casino Action from Anywhere
Live casino games bring the atmosphere of a brick-and-mortar venue directly to your screen. Streamed in HD and hosted by professional dealers, these games offer immersive, real-time interaction for a more social gaming experience.
- Live Blackjack & Roulette – Popular staples, enhanced with side bets, custom tables, and modern variants like Infinite Blackjack or Lightning Roulette.
- Baccarat & Live Game Shows – Enjoy fast-paced baccarat rounds or participate in TV-style games such as Crazy Time, Monopoly Live, or Deal or No Deal Live.
- Trusted Providers – Evolution Gaming and Pragmatic Play Live lead the industry with intuitive interfaces, smooth streaming, and world-class production values.
Live games appeal to players looking for interactive, high-stakes excitement combined with the convenience of playing from home.
Specialty Games: Beyond the Traditional Casino Format
Non GamStop casinos go the extra mile by offering unique gaming alternatives that cater to niche interests and casual players alike.
- Scratch Cards & Instant Win Games – Quick, easy, and often surprisingly rewarding.
- Virtual Sports – Simulated matches in football, horse racing, and other sports allow for 24/7 betting with realistic graphics and fast results.
- Provably Fair Games – Blockchain-powered games that let players verify fairness for full transparency, ideal for crypto-savvy gamblers.
These alternatives help round out the gaming portfolio and keep things fresh for players looking to try something different.
Leading Game Developers Behind the Scenes
The game selection at non GamStop casinos is made possible by partnerships with some of the most respected names in iGaming. These providers are known for innovation, reliability, and variety:
- Pragmatic Play – Creators of high-RTP slots and engaging live dealer tables.
- Evolution Gaming – The gold standard in live casino software, with cutting-edge interactive features.
- Nolimit City – Pioneers of high-volatility slots with bold designs and unique mechanics.
- Hacksaw Gaming – Known for modern, mobile-optimized slots and innovative formats.
- NetEnt & Playtech – Industry veterans with iconic games and consistently high-quality releases.
With constant updates and new releases, these developers ensure non GamStop casinos stay ahead of the curve and keep players engaged.
Something for Every Player
From high-stakes action to casual fun, non GamStop casinos offer unmatched variety and flexibility. Whether you’re chasing big jackpots, practicing strategy at the tables, or enjoying the thrill of live gaming, you’ll find a wealth of options designed to suit every playstyle. Backed by top-tier providers and packed with innovative features, these platforms deliver an online casino experience that goes beyond the ordinary.
Top Casino Bonuses You’ll Find at Non GamStop Sites
Bonuses and promotions are one of the biggest advantages of playing at non GamStop casinos. These sites offer players a wider selection of lucrative deals than UKGC-regulated platforms—thanks to fewer restrictions and more generous terms. Whether you’re after massive welcome packages, risk-free no deposit offers, or crypto-exclusive rewards, non GamStop casinos are packed with opportunities to boost your bankroll and extend gameplay.
First-Time Deposit Offers: Kickstart Your Gaming With a Bang
Welcome bonuses at non GamStop casinos are designed to impress. These packages typically offer high-percentage match bonuses on your initial deposits—sometimes stretching over multiple top-ups—and are often bundled with a healthy dose of free spins.
- Typical Offer: 200% bonus up to €1,000 + 100 free spins on popular slots.
- Why It Stands Out: Larger bonus caps and more spins than UK casinos allow you to explore games with extra cash.
- Key Tip: Check the wagering terms, which usually range from 30x to 50x, though some casinos offer lower or even zero-wager options.
These bonuses are ideal for newcomers looking to maximize their first deposit and try out a variety of games with minimal risk.
No Deposit Rewards: Try Before You Commit
No deposit bonuses are a fan-favorite at non GamStop casinos, offering free spins or small cash credits simply for signing up—no deposit required.
- Common Deal: €10 free or 50 spins on registration.
- Why It’s Great: You can play for real money without funding your account first.
- Keep in Mind: These offers often have wagering requirements and caps on withdrawable winnings.
Perfect for players who want to explore a new site with zero financial commitment.
Free Spins Promotions: More Spins, More Wins
Free spins are a regular feature across non GamStop platforms and are commonly tied to welcome packages, reload bonuses, or weekly promotions.
- What to Expect: 100 free spins on titles like Book of Dead with a qualifying deposit.
- Why You’ll Love It: Try out popular slots and cash out real winnings if you meet the playthrough terms.
- Best For: Slot fans looking to increase their playtime without increasing their risk.
These promotions are often game-specific, so they’re also a great way to discover trending slots or new releases.
Crypto Bonuses: Bigger Perks for Digital Currency Players
Many non GamStop casinos support crypto payments and reward users with exclusive crypto deposit offers. These bonuses often include higher match percentages, lower wagering rules, and faster payout times.
- Offer Example: 300% crypto bonus up to €5,000 for Bitcoin deposits.
- Why It’s Smart: Crypto transactions come with enhanced privacy, fewer fees, and instant processing.
- Ideal For: Players who use Bitcoin, Ethereum, or altcoins and want better value for their deposits.
If you’re already using crypto, these bonuses are a no-brainer for maximizing value.
Cashback Deals: Win Back a Portion of Your Losses
Cashback bonuses are becoming increasingly popular at non GamStop sites. These promotions give players a percentage of their net losses back, often with no wagering requirements.
- Typical Offer: 10% cashback weekly with zero wagering.
- Why It Matters: Even if luck isn’t on your side, you get a second shot with real money.
- Best For: Frequent players and high rollers looking to soften the impact of a bad streak.
Cashback deals provide consistent value, especially for those who play often and appreciate ongoing risk mitigation.
Reload Bonuses: Extra Value for Returning Players
Reload bonuses reward loyalty by offering match bonuses on future deposits, not just your first. These promotions encourage consistent play and help maintain your bankroll over time.
- Example Bonus: 50% reload up to €500 every Monday.
- Why You Should Care: They’re perfect for players who deposit regularly and want ongoing incentives.
- Works Best For: Long-term players looking to extend their balance beyond the initial welcome deal.
Reload deals show that non GamStop casinos value player retention, not just acquisition.
VIP Clubs & Loyalty Programs: Elite Perks for Dedicated Players
Loyal players are often invited to join exclusive VIP clubs or tier-based loyalty schemes at non GamStop casinos. These programs reward continued play with tailored perks and enhanced benefits.
- Program Example: Multi-level VIP system with increasing benefits like higher withdrawal limits, personalized support, and monthly cashback up to 25%.
- Why It’s Worth It: Get access to priority support, custom bonuses, and faster cashouts.
- Best For: High-stakes players or anyone planning to stick with one casino long-term.
If you’re a committed player, joining a VIP program can significantly enhance your overall experience.
Unlock More Value with Non GamStop Casino Bonuses
From no-risk no deposit bonuses to massive crypto rewards and VIP exclusives, non GamStop casinos deliver a bonus system that’s flexible, generous, and player-friendly. With fewer restrictions and more creative promotions than their UK-licensed counterparts, these platforms offer serious value for players of all levels.
Before claiming, always review bonus terms and conditions, especially wagering requirements and withdrawal limits, to make sure you’re getting the most out of your promotions.
Final Thoughts: The Advantages of Choosing Non GamStop Casinos
Non GamStop online casinos deliver a gaming experience that’s both flexible and full of variety—making them an ideal option for players seeking more freedom than UKGC-licensed platforms can offer. From thousands of cutting-edge slot games and classic table titles to immersive live dealer rooms, these casinos provide an expansive library tailored to all player preferences.
What truly sets them apart, though, are the generous bonuses and player-centric features. You’ll find welcome packages with high match percentages, risk-free no deposit deals, free spins galore, and exclusive crypto-friendly promotions—all designed to maximize value and extend your playtime.
Beyond games and bonuses, non GamStop sites stand out for their unrestricted policies and versatile payment options. Whether you’re a casual player or a seasoned high roller, you’ll benefit from:
- Flexible banking methods, including fast crypto deposits and withdrawals
- Fewer limitations on stakes, deposits, and cashouts
- Access to tiered VIP programs and loyalty rewards for long-term players
- A wider variety of games, including those not available on UKGC sites
- These features allow players to take full control of their online gambling experience—without the usual red tape.
If you’re looking for a platform that combines diverse gameplay, better promotions, and fewer restrictions, then non GamStop casinos are well worth exploring. Whether your goal is to chase high-volatility jackpots, enjoy casual spins, or take advantage of crypto bonuses, these sites offer the tools and freedom to tailor your gaming experience exactly how you like it.
Just remember: Always choose reputable platforms, read the terms and conditions carefully, and play responsibly to get the most from your time online.
Frequently Asked Questions
-
What is a non GamStop online casino?
A non GamStop online casino is a gambling platform that operates outside the UK Gambling Commission (UKGC) and is not registered with the GamStop self-exclusion program. These casinos offer greater flexibility, fewer restrictions, and access to a broader range of games, bonuses, and payment methods.
-
Are non GamStop casinos legal for UK players?
Yes, UK players can legally access and play at non GamStop casinos. While these sites aren’t licensed by the UKGC, they are often licensed by reputable international regulators such as Curaçao eGaming or Malta Gaming Authority.
-
What are the main advantages of playing at a non GamStop casino?
Non GamStop casinos offer more generous bonuses, fewer restrictions on betting limits, broader payment options (including crypto), and access to international game providers not available on UK-regulated sites.
-
Can I use UK payment methods at non GamStop casinos?
Yes, many non GamStop casinos accept UK-friendly payment methods like Visa, Mastercard, Skrill, Neteller, and even mobile solutions like Apple Pay and Google Pay. However, some UK banks may restrict transactions to offshore gambling sites.
-
Are cryptocurrency payments accepted at non GamStop casinos?
Absolutely. Non GamStop casinos frequently support Bitcoin, Ethereum, Litecoin, and Tether. Crypto payments are fast, secure, and often come with exclusive bonuses or lower fees.
-
What types of bonuses do non GamStop casinos offer?
Bonuses include generous welcome packages, no deposit bonuses, free spins, reload offers, cashback promotions, and VIP rewards. Many come with higher limits and more flexible wagering terms compared to UKGC-regulated casinos.
-
Do non GamStop casinos offer no deposit bonuses?
Yes, many non GamStop platforms provide no deposit bonuses—such as free spins or small cash rewards—just for signing up. These allow players to explore the site and potentially win without depositing.
-
Is it safe to play at non GamStop casinos?
It can be, as long as you choose reputable sites with valid licensing, secure encryption, and transparent terms. Look for platforms with verified payment options and positive player reviews for added assurance.
-
What kinds of games are available at non GamStop casinos?
Players can enjoy thousands of games, including video slots, jackpot slots, blackjack, roulette, baccarat, poker, live dealer games, scratch cards, virtual sports, and even provably fair blockchain games.
-
Who are the top software providers at non GamStop casinos?
Popular developers include Pragmatic Play, Evolution Gaming, Nolimit City, Hacksaw Gaming, NetEnt, and Playtech. These providers ensure high-quality graphics, unique features, and engaging gameplay.
-
Are there live dealer games at non GamStop casinos?
Yes, most non GamStop casinos offer live dealer games streamed in HD, including blackjack, roulette, baccarat, and interactive game shows like Crazy Time and Monopoly Live.
-
How fast are withdrawals at non GamStop casinos?
Withdrawal speed varies by method. E-wallets and cryptocurrencies usually process within hours, while bank transfers can take several business days. Always check the casino’s withdrawal terms beforehand.
-
Can I self-exclude at a non GamStop casino?
Most non GamStop casinos have their own self-exclusion tools, but they are not part of the UK-wide GamStop network. If you’re struggling with gambling, consider sites with responsible gaming features or seek third-party help.
-
Are non GamStop casinos mobile-friendly?
Yes, the majority of non GamStop platforms are optimized for smartphones and tablets. Many also support mobile payment methods and offer a seamless gaming experience on both iOS and Android.
-
How do I choose the best non GamStop casino?
Look for platforms with a valid gaming license, strong security features, diverse game libraries, attractive bonuses, and trusted payment options. Reading player reviews and comparing welcome offers can also help you make an informed choice.


